What Parent Function Goes Up Down and Up Again on a Graph
| Basic Parent Functions | Writing Transformed Equations from Graphs |
| Generic Transformations of Functions | Rotational Transformations |
| Vertical Transformations | Transformations of Inverse Functions |
| Horizontal Transformations | Applications of Parent Office Transformations |
| Mixed Transformations | More Exercise |
| Transformations Using Functional Notation |
For Absolute Value Transformations, see theAbsolute Value Transformations section. Here are links to Parent Function Transformations in other sections: Transformations of Quadratic Functions (quick and easy way);Transformations of Radical Functions;Transformations of Rational Functions; Transformations of Exponential Functions;Transformations of Logarithmic Functions; Transformations of Piecewise Functions; Transformations of Trigonometric Functions; Transformations of Inverse Trigonometric Functions
Y'all may not be familiar with all the functions and characteristics in the tables; here are some topics to review:
- Whether functions are fifty-fifty, odd, or neither, discussed here in the Advanced Functions: Compositions, Even and Odd, and Extrema.
- End behavior and asymptotes, discussed in the Asymptotes and Graphing Rational Functions and Graphing Polynomials sections
- Exponential and Logarithmic Functions
- Trigonometric Functions
Basic Parent Functions
You'll probably study some "popular" parent functions and piece of work with these to learn how to transform functions – how to move and/or resize them. We phone call these basic functions "parent" functions since they are the simplest form of that type of function, meaning they are as close as they can get to the origin \(\left( {0,0} \right)\).
The nautical chart below provides some basic parent functions that y'all should be familiar with. I've also included the pregnant points, or disquisitional points, the points with which to graph the parent function. I also sometimes call these the "reference points" or "anchor points".
Know the shapes of these parent functions well! Even when using t -charts, yous must know the general shape of the parent functions in order to know how to transform them correctly!
| Parent Role | Graph | Parent Function | Graph |
| \(y=x\) Domain: \(\left( {-\infty ,\infty } \right)\) Cease Behavior**: Critical points: \(\displaystyle \left( {-1,-1} \right),\,\left( {0,0} \right),\,\left( {1,1} \right)\) |  | \(y=\left| 10 \right|\) Domain: \(\left( {-\infty ,\infty } \right)\) Finish Behavior: Critical points: \(\displaystyle \left( {-1,1} \right),\,\left( {0,0} \right),\,\left( {1,1} \right)\) |  |
| \(y={{ten}^{2}}\) Domain: \(\left( {-\infty ,\infty } \right)\) End Beliefs: Critical points: \(\displaystyle \left( {-1,1} \right),\,\left( {0,0} \right),\,\left( {1,1} \right)\) |  | \(y=\sqrt{10}\) Domain: \(\left[ {0,\infty } \right)\) End Beliefs: \(\displaystyle \begin{array}{l}x\to 0,\,\,\,\,y\to 0\\x\to \infty \text{,}\,\,y\to \infty \terminate{assortment}\) Critical points: \(\displaystyle \left( {0,0} \right),\,\left( {ane,one} \right),\,\left( {4,2} \right)\) |  |
| \(y={{10}^{three}}\) Domain: \(\left( {-\infty ,\infty } \right)\) End Behavior: Critical points: \(\displaystyle \left( {-ane,-1} \correct),\,\left( {0,0} \right),\,\left( {1,1} \right)\) |  | \(y=\sqrt[3]{ten}\) Domain: \(\left( {-\infty ,\infty } \right)\) End Behavior: Disquisitional points: \(\displaystyle \left( {-1,-one} \right),\,\left( {0,0} \right),\,\left( {1,ane} \right)\) |  |
| \(\begin{array}{c}y={{b}^{x}},\,\,\,b>1\,\\(\text{Instance:}\,\,y={{2}^{ten}})\cease{array}\) Exponential, Neither Domain: \(\left( {-\infty ,\infty } \right)\) End Behavior: Critical points: \(\displaystyle \left( {-1,\frac{1}{b}} \right),\,\left( {0,one} \right),\,\left( {ane,b} \right)\) Asymptote: \(y=0\) |  | \(\begin{array}{c}y={{\log }_{b}}\left( x \right),\,\,b>1\,\,\,\\(\text{Example:}\,\,y={{\log }_{2}}x)\finish{array}\) Log, Neither Domain: \(\left( {0,\infty } \correct)\) Terminate Beliefs: Critical points: \(\displaystyle \left( {\frac{i}{b},-i} \right),\,\left( {1,0} \right),\,\left( {b,1} \correct)\) Asymptote: \(10=0\) |  |
| \(\displaystyle y=\frac{1}{x}\) Rational (Changed), Odd Domain: \(\left( {-\infty ,0} \correct)\cup \left( {0,\infty } \right)\) Terminate Beliefs: Critical points: \(\displaystyle \left( {-1,-1} \right),\,\left( {one,1} \right)\) Asymptotes: \(y=0,\,\,x=0\) **Notation that this function is the inverse of itself! |  | \(\displaystyle y=\frac{one}{{{{x}^{2}}}}\) Rational (Changed Squared), Fifty-fifty Domain: \(\left( {-\infty ,0} \right)\loving cup \left( {0,\infty } \correct)\) Cease Behavior: Critical points: \(\displaystyle \left( {-1,\,one} \right),\left( {1,1} \right)\) Asymptotes: \(x=0,\,\,y=0\) |  |
| \(y=\text{int}\left( x \right)=\left\lfloor x \right\rfloor \) Greatest Integer* , Neither Domain: \(\left( {-\infty ,\infty } \correct)\) End Behavior: Disquisitional points: \(\displaystyle \begin{assortment}{l}x:\left[ {-1,0} \correct)\,\,\,y:-1\\10:\left[ {0,i} \right)\,\,\,y:0\\x:\left[ {1,2} \right)\,\,\,y:i\end{array}\) |  | \(y=C\) (\(y=2\)) Constant, Even Domain: \(\left( {-\infty ,\infty } \correct)\) End Behavior: Critical points: \(\displaystyle \left( {-i,C} \correct),\,\left( {0,C} \correct),\,\left( {ane,C} \right)\) | |
*The Greatest Integer Function, sometimes called the Pace Function, returns the greatest integer less than or equal to a number (think of rounding down to an integer). There's also a To the lowest degree Integer Role, indicated by \(y=\left\lceil x \correct\rceil \), which returns the least integer greater than or equal to a number (think of rounding up to an integer).
**Notes on End Behavior: To get theend behavior of a office, we just look at thesmallest andlargest values of \(x\), and see which way the \(y\) is going. Not all functions have terminate behavior defined; for example, those that go back and forth with the \(y\) values (called "periodic functions") don't have cease behaviors.
Nigh of the time, our stop beliefs looks something similar this: \(\displaystyle \begin{array}{50}ten\to -\infty \text{, }\,y\to \,\,?\\x\to \infty \text{, }\,\,\,y\to \,\,?\stop{array}\) and we have to fill in the \(y\) part. For example, the end beliefs for a line with a positive slope is: \(\begin{array}{l}x\to -\infty \text{, }\,y\to -\infty \\ten\to \infty \text{, }\,\,\,y\to \infty \terminate{array}\), and the terminate beliefs for a line with a negative slope is: \(\begin{array}{l}x\to -\infty \text{, }\,y\to \infty \\x\to \infty \text{, }\,\,\,y\to -\infty \end{assortment}\). One way to retrieve of stop behavior is that for \(\displaystyle x\to -\infty \), nosotros expect at what's going on with the \(y\) on the left-hand side of the graph, and for \(\displaystyle x\to \infty \), we await at what's happening with \(y\) on the right-paw side of the graph.
There are a couple of exceptions; for case, sometimes the \(x\) starts at 0 (such as in theradical office), we don't take the negative portion of the \(ten\) end behavior. Also, when \(x\) starts very close to 0 (such as in in thelog function), we bespeak that \(x\) is starting from the positive (right) side of 0 (and the \(y\) is going down); we indicate this by \(\displaystyle x\to {{0}^{+}}\text{, }\,y\to -\infty \).
Generic Transformations of Functions
Once more, the "parent functions" assume that nosotros have the simplest class of the function; in other words, the function either goes through the origin \(\left( {0,0} \correct)\), or if it doesn't go through the origin, information technology isn't shifted in whatsoever way. When a function is shifted, stretched (or compressed), or flipped in any way from its "parent function", it is said to exist transformed, and is a transformation of a function.
T-charts are extremely useful tools when dealing with transformations of functions. For example, if you know that the quadratic parent role \(y={{x}^{two}}\) is being transformed ii units to the correct, and 1 unit of measurement downwards (only a shift, not a stretch or a flip), we can create the original t -chart, following by the transformation points on the exterior of the original points. So we can plot the "outside" (new) points to get the newly transformed function:
| Transformation | T-chart | Graph | ||||||||
| Quadratic Function \(y={{x}^{ii}}\) Transform function 2 units to the right, and one unit of measurement downwards. This turns into the function \(y={{\left( {x-two} \correct)}^{2}}-1\), oddly enough! |
Transformed: Domain: \(\left( {-\infty ,\infty } \right)\) Range: \(\left[ {-one,\,\,\infty } \right)\) |  |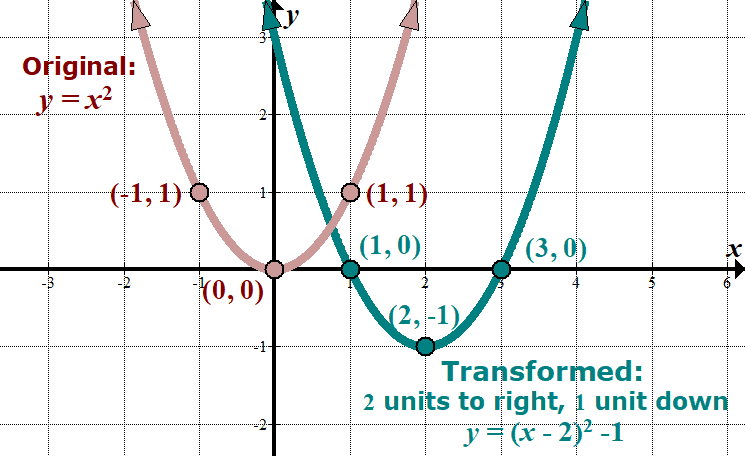
When looking at the equation of the transformed office, however, we have to exist conscientious. When functions are transformed on the exterior of the \(f(x)\) part, you move the function up and down and do the "regular" math, as we'll see in the examples beneath. These are vertical transformations or translations, and bear upon the \(y\) part of the function. When transformations are made on the within of the \(f(x)\) part, you movement the part dorsum and along (but practice the "opposite" math – since if y'all were to isolate the \(x\), y'all'd motion everything to the other side). These are horizontal transformations or translations, and affect the \(x\) part of the function.
There are several ways to perform transformations of parent functions; I like to use t -charts , since they work consistently with ever function. And note that in nigh t-charts, I've included more than simply the critical points above, merely to evidence the graphs better.
Vertical Transformations
Here are the rules and examples of when functions are transformed on the "outside" (notice that the \(y\)values are affected). The t-charts include the points (ordered pairs) of the original parent functions, and also the transformed or shifted points. The outset ii transformations are translations, the third is a dilation, and the last are forms of reflections. Absolute value transformations will be discussed more expensively in the Absolute Value Transformations Department!
| Trans formation | What It Does | Example | Graph | ||||||||
| \(f\left( ten \right)+b\) Translation | Move graph up \(b\) units Every betoken on the graph is shifted up \(b\) units. The \(x\)'s stay the same; add \(b\) to the \(y\) values. | Parent: \(y={{x}^{2}}\) Transformed: \(y={{10}^{2}}+ \,2\)
| Domain: \(\left( {-\infty ,\infty } \correct)\) Range: \(\left[ {2,\infty } \correct)\) | ||||||||
| \(f\left( 10 \right)-b\) Translation | Motility graph downward \(b\) units Every point on the graph is shifted downwards \(b\) units. The \(x\)'s stay the same; subtract \(b\) from the \(y\) values. | Parent: \(y=\sqrt{x}\) Transformed: \(y=\sqrt{x}- \,3\)
| | ||||||||
| \(a\,\cdot f\left( x \correct)\) Dilation | Stretch graph vertically past a scale factor of \(a\) (sometimes called a dilation). Note that if \(a<1\), the graph is compressed or shrunk. Every bespeak on the graph is stretched \(a\) units. The \(x\)'south stay the same; multiply the \(y\) values by \(a\). | Parent: \(y={{ten}^{3}}\) Transformed: \(y={{4x}^{three}}\)
| | ||||||||
| \(-f\left( x \right)\) Reflection | Flip graph effectually the \(ten\)-centrality. Every point on the graph is flipped vertically. The \(10\)'s stay the same; multiply the \(y\) values by \(-1\). | Parent: \(y=\left| x \right|\) Transformed: \(y=-\left| x \right|\)
| | ||||||||
| \(\left| {f\left( x \right)} \right|\) Absolute Value on the \(y\) (More examples hither in the Absolute Value Transformation section) | Reflect part of graph underneath the \(x\)-centrality (negative \(y\)'south) across the \(10\)-axis. Leave positive \(y\)'s the same. The \(10\)'s stay the same; have the absolute value of the \(y\)'s. | Parent: \(y=\sqrt[three]{ten}\) Transformed: \(y=\left| {\sqrt[3]{x}} \right|\)
|  Domain: \(\left( {-\infty ,\infty } \correct)\) Range:\(\left[ {0,\infty } \correct)\) |
Domain: \(\left[ {0,\infty } \right)\) Range: \(\left[ {-3,\infty } \correct)\)
Domain: \(\left( {-\infty ,\infty } \correct)\)Range: \(\left( {-\infty ,\,\infty } \correct)\)
Domain: \(\left( {-\infty ,\infty } \right)\)Range: \(\left( {-\infty\,,0} \right]\)Horizontal Transformations
Here are the rules and examples of when functions are transformed on the "inside" (notice that the \(ten\)-values are affected). Observe that when the \(x\)-values are affected, you do the math in the "opposite" way from what the part looks like: if you're calculation on the inside, you subtract from the \(ten\); if y'all're subtracting on the within, you add to the \(x\); if you're multiplying on the inside, y'all divide from the \(x\); if yous're dividing on the inside, yous multiply to the \(x\). If you accept a negative value on the inside, y'all flip across the \(\boldsymbol{y}\) axis (notice that you lot still multiply the \(x\) by \(-1\) but similar y'all do for with the \(y\) for vertical flips). The start two transformations are translations, the tertiary is a dilation, and the last are forms of reflections.
Absolute value transformations will be discussed more than expensively in the Absolute Value Transformations Section!
(You may notice it interesting is that a vertical stretch behaves the aforementioned mode as a horizontal pinch, and vice versa, since when stretch something upwards, we are making it skinnier.)
| Trans formation | What It Does | Case | Graph | ||||||||||||
| \(f\left( {10+b} \correct)\) Translation | Move graph left \(b\) units (Do the "reverse" when change is within the parentheses or underneath radical sign.) Every bespeak on the graph is shifted left \(b\) units. The \(y\)'due south stay the same; decrease \(b\) from the \(ten\) values. | Parent: \(y={{x}^{2}}\) Transformed: \(y={{\left( {10+2} \right)}^{2}}\)
| | ||||||||||||
| \(f\left( {10-b} \correct)\) Translation | Move graph correct \(b\) units Every point on the graph is shifted right \(b\) units. The \(y\)'south stay the same; add \(b\) to the \(ten\) values. | Parent: \(y=\sqrt{x}\) Transformed: \(y=\sqrt{{x- \,3}}\)
| | ||||||||||||
| \(f\left( {a\cdot x} \correct)\) Dialation | Shrink graph horizontally by a scale factor of \(a\) units (stretch or multiply by \(\displaystyle \frac{1}{a}\)) Every point on the graph is compressed \(a\) units horizontally. The \(y\)'s stay the aforementioned; multiply the \(x\)-values by \(\displaystyle \frac{one}{a}\). | Parent: \(y={{10}^{iii}}\) T ransformed: \(y={{\left( {4x} \right)}^{three}}\)
| | ||||||||||||
| \(f\left( {-x} \correct)\) Reflection | Flip graph around the \(y\)-axis Every bespeak on the graph is flipped around the \(y\) axis. The \(y\)'south stay the same; multiply the \(ten\)-values by \(-1\). | Parent: \(y=\sqrt{10}\) Transformed: \(y=\sqrt{{-x}}\)
| | ||||||||||||
| \(f\left( {\left| ten \correct|} \right)\) Absolute Value on the \(x\) (More than examples here in the Absolute Value Transformation section) | "Throw away" the negative \(10\)'south; reverberate the positive \(x\)'s across the \(y\)-axis. The positive \(x\)'southward stay the same; the negative \(x\)'southward accept on the \(y\)'south of the positive \(x\)'s. | Parent: \(y=\sqrt{x}\) Transformed: \(y=\sqrt{{\left| x \right|}}\)
|  Domain: \(\left( {-\infty ,\infty } \right)\)Range:\(\left[ {0,\infty } \right)\) |
Domain: \(\left( {-\infty ,\infty } \right)\)Range: \(\left[ {0,\infty } \right)\)
Domain: \(\left[ {-3,\infty } \right)\)Range: \(\left[ {0,\infty } \correct)\)
Domain: \(\left( {-\infty ,\infty } \correct)\)Range: \(\left( {-\infty ,\infty } \correct)\)
Domain: \(\left( {-\infty ,0} \right]\)Range: \(\left[ {0,\infty } \right)\)Mixed Transformations
Most of the problems you'll become will involve mixed transformations, or multiple transformations, and we practise need to worry most the gild in which we perform the transformations. Information technology usually doesn't matter if nosotros make the \(x\) changes or the \(y\) changes start, merely within the \(x\)'south and \(y\)'southward, nosotros need to perform the transformations in the order below. Note that this is sort of like to the society with PEMDAS(parentheses, exponents, multiplication/division, and improver/subtraction). When performing these rules, the coefficients of the inside \(x\) must be ane ; for example, we would need to have \(y={{\left( {4\left( {x+ii} \right)} \right)}^{two}}\) instead of \(y={{\left( {4x+eight} \right)}^{2}}\) (by factoring). If you didn't larn information technology this way, encounter Important Note beneath.
Hither is the club. We can do steps 1 and ii together (order doesn't actually matter), since nosotros can think of the first two steps as a "negative stretch/pinch."
- Perform Flipping across the axes first (negative signs).
- Perform Stretching and Shrinking next (multiplying and dividing).
- Perform Horizontal and Vertical shifts concluding (adding and subtracting).
I like to take the critical points and maybe a few more points of the parent functions, and perform all thetransformations at the same time with a t-chart! Nosotros but practice the multiplication/partition kickoff on the \(x\) or \(y\) points, followed by addition/subtraction. Information technology makes it much easier!Note again that since we don't take an \(\boldsymbol {x}\) "by itself" (coefficient of i) on the inside, we take to get it that manner by factoring! For example,we'd have to alter \(y={{\left( {4x+eight} \correct)}^{two}}\text{ to }y={{\left( {4\left( {ten+2} \right)} \correct)}^{2}}\).
Permit'due south endeavour to graph this "complicated" equation and I'll show you how easy information technology is to practice with a t-chart: \(\displaystyle f(ten)=-three{{\left( {2x+8} \right)}^{2}}+10\). (Note that for this example, nosotros could move the \({{two}^{2}}\) to the outside to get a vertical stretch of \(iii\left( {{{2}^{2}}} \right)=12\), but we tin't do that for many functions.) We first demand to become the \(x\) past itself on the inside by factoring, so we tin can perform the horizontal translations. This is what we end upwardly with: \(\displaystyle f(x)=-3{{\left( {2\left( {ten+iv} \right)} \right)}^{2}}+10\). Look at what'southward done on the "exterior" (for the \(y\)'due south) and make all the moves at one time, past post-obit the exact math. And then look at what we practise on the "inside" (for the \(ten\)'s) and make all the moves at in one case, but practice the opposite math. Nosotros exercise this with a t -chart.
Start with the parent role \(f(10)={{ten}^{2}}\). If nosotros look at what we're doing on the outside of what is being squared, which is the \(\displaystyle \left( {2\left( {x+4} \correct)} \right)\), we're flipping it across the \(10\)-axis (the minus sign), stretching information technology past a gene of three , and calculation 10 (shifting up 10 ). These are the things that nosotros are doing vertically, or to the \(y\). If nosotros look at what we are doing on the inside of what we're squaring, we're multiplying it by two , which ways nosotros take to divide by 2 (horizontal compression by a factor of \(\displaystyle \frac{1}{two}\)), and we're adding four , which means we take to decrease four (a left shift of four ). Remember that nosotros do the opposite when nosotros're dealing with the \(x\). Too remember that nosotros e'er have to practise the multiplication or division kickoff with our points, and then the adding and subtracting (sort of similar PEMDAS).
Here is the t-nautical chart with the original function, and and then the transformations on the outsides. Now we can graph the exterior points (points that aren't crossed out) to get the graph of the transformation. I've also included an caption of how to transform this parabola without a t-chart, as nosotros did in the Introduction to Quadratics section here.
| t-nautical chart | Transformed Graph | ||||||||||||
| Parent: \(y={{10}^{2}}\) (Quadratic) Transformed:\(\displaystyle f(10)=-3{{\left( {2\left( {x+four} \right)} \right)}^{2}}+x\) y changes:\(\displaystyle f(x)=\color{blue}{{-3}}{{\left( {2\left( {ten+4} \right)} \right)}^{2}}\color{blue}{+10}\) x changes: \(\displaystyle f(x)=-iii{{\left( {\color{bluish}{2}\left( {x\text{ }\color{blue}{{+\text{ }4}}} \correct)} \right)}^{ii}}+10\) Contrary for \(x\), "regular" for \(y\), multiplying/dividing beginning: Coordinate Rule: \(\left( {x,\,y} \correct)\to \left( {.5x-4,-3y+ten} \right)\)
|  Domain: \(\left( {-\infty ,\infty } \right)\) Range: \(\left( {-\infty ,10} \right]\) | ||||||||||||
| How to graphwithout a t-chart: \(\displaystyle f(x)=-iii{{\left( {2\left( {x+iv} \right)} \right)}^{two}}+10\) Since this is a parabola and it's in vertex form (\(y=a{{\left( {x-h} \right)}^{two}}+k,\,\,\left( {h,chiliad} \right)\,\text{vertex}\)), the vertex of the transformation is \(\left( {-4,10} \correct)\). Discover that the coefficient of is –12 (by moving the \({{2}^{2}}\) outside and multiplying it past the –iii ). And so the vertical stretch is 12 , and the parabola faces down because of the negative sign. The parent graph quadratic goes up 1 and over (and back) one to go two more than points, merely with a vertical stretch of 12 , nosotros become over (and back) 1 and down 12 from the vertex. Now we accept ii points from which you can describe the parabola from the vertex. | |||||||||||||
IMPORTANT Note:In some books, for \(\displaystyle f\left( ten \right)=-3{{\left( {2x+viii} \right)}^{2}}+x\) , they may NOT have yous factor out the2 on the inside, just just switch the lodge of the transformation on the \(\boldsymbol{ten}\).
In this instance, the society of transformations would exist horizontal shifts, horizontal reflections/stretches, vertical reflections/stretches, and then vertical shifts. For example, for this problem, you would move to the left viii first for the \(\boldsymbol{10}\), and and then compress with a factor of \(\displaystyle \frac {1}{2}\) for the \(\boldsymbol{x}\) (which is opposite of PEMDAS). Then you would perform the \(\boldsymbol{y}\) (vertical) changes the regular style: reverberate and stretch by iii first, and then shift up ten. So, you lot would have \(\displaystyle {\left( {x,\,y} \right)\to \left( {\frac{ane}{two}\left( {x-8} \right),-3y+10} \right)}\). Try a t-chart; you'll get the aforementioned t-chart as in a higher place!
More Examples of Mixed Transformations:
Here are a couple more examples (using t -charts), with different parent functions. Don't worry if you are totally lost with the exponential and log functions; they will be discussed in the Exponential Functions and Logarithmic Functions sections. Also, the last type of function is a rational function that will exist discussed in the Rational Functions section.
| Transformation | T-nautical chart/Domain and Range | Graph | ||||||||
| \(\displaystyle y=\frac{three}{2}{{\left( {-x} \right)}^{three}}+two\) Parent function: \(y={{x}^{3}}\) For this function, notation that could have also put the negative sign on the outside (thus affecting the \(y\)), and we would have gotten the aforementioned graph. |
Domain: \(\left( {-\infty ,\infty } \right)\) Range:\(\left( {-\infty ,\infty } \right)\) |  | ||||||||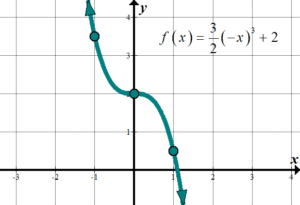
| \(\displaystyle y=\frac{i}{2}\sqrt{{-10}}\) Parent role: \(y=\sqrt{ten}\) |
Domain: \(\left( {-\infty ,0} \right]\) Range:\(\left[ {0,\infty } \correct)\) |  | ||||||||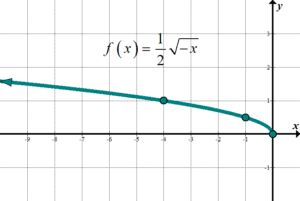
| \(y={{2}^{{10-four}}}+iii\) Parent function: \(y={{2}^{x}}\) For exponential functions, utilize –1 , 0 , and 1 for the \(ten\) values for the parent part. (Piece of cake way to remember: exponent is like \(x\)). |
Domain: \(\left( {-\infty ,\infty } \right)\) Range:\(\left( {3,\infty } \correct)\) Asymptote: \(y=iii\) |  | ||||||||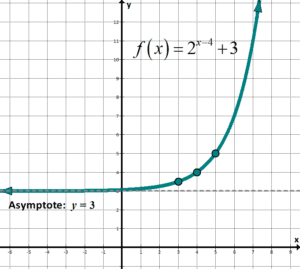
| \(\brainstorm{assortment}{fifty}y=\log \left( {2x-2} \right)-one\\y=\log \left( {2\left( {x-one} \right)} \right)-1\stop{array}\) Parent function: \(y=\log \left( x \right)={{\log }_{{10}}}\left( x \right)\) For log and ln functions, use – 1 , 0 , and 1 for the \(y\) values for the parent office For example, for \(y={{\log }_{three}}\left( {2\left( {x-i} \right)} \right)-1\), the \(x\) values for the parent function would be \(\displaystyle \frac{i}{3},\,i,\,\text{and}\,3\).) |
Domain: \(\left( {one,\infty } \right)\) Range:\(\left( {-\infty ,\infty } \right)\) Asymptote: \(x=1\) |  | ||||||||
| \(\displaystyle y=\frac{iii}{{two-ten}}\,\,\,\,\,\,\,\,\,\,\,y=\frac{3}{{-\left( {ten-2} \right)}}\) Parent function: \(\displaystyle y=\frac{1}{x}\) For this function, note that could have likewise put the negative sign on the outside (thus, used \(x+2\) and \(-3y\)). |
Domain:\(\left( {-\infty ,2} \right)\loving cup \left( {2,\infty } \right)\) Range:\(\left( {-\infty ,0} \right)\cup \left( {0,\infty } \right)\) Asymptotes: \(y=0\) and \(x=2\) |  |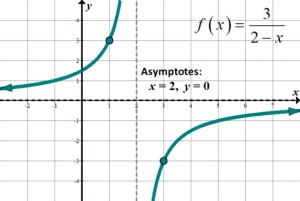
Here'due south a mixed transformation with the Greatest Integer Function (sometimes chosen the Floor Function). Annotation how we can use intervals equally the \(x\) values to brand the transformed function easier to draw:
| Transformation | T-chart/Domain and Range | Graph | ||||||||||||
| \(\displaystyle y=\left[ {\frac{ane}{ii}x-two} \right]+iii\) \(\displaystyle y=\left[ {\frac{1}{2}\left( {x-4} \right)} \right]+3\) Parent function: \(y=\left[ x \right]\) Notation how we had to accept out the \(\displaystyle \frac{one}{ii}\) to make information technology in the right grade. |
Domain:\(\left( {-\infty ,\infty } \right)\) Range:\(\{y:y\in \mathbb{Z}\}\text{ (integers)}\) |  |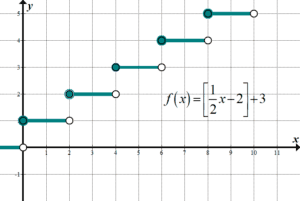
Transformations Using Functional Notation
You might meet mixed transformations in the grade \(\displaystyle m\left( x \right)=a\cdot f\left( {\left( {\frac{1}{b}} \correct)\left( {x-h} \correct)} \right)+1000\), where \(a\) is the vertical stretch, \(b\) is the horizontal stretch, \(h\) is the horizontal shift to the right, and \(k\) is the vertical shift upwards. In this case, we have the coordinate rule \(\displaystyle \left( {x,y} \correct)\to \left( {bx+h,\,ay+thousand} \correct)\). For case, for the transformation \(\displaystyle f(ten)=-three{{\left( {two\left( {x+iv} \right)} \right)}^{2}}+10\), we accept \(a=-3\), \(\displaystyle b=\frac{1}{2}\,\,\text{or}\,\,.5\), \(h=-4\), and \(k=10\). Our transformation \(\displaystyle thou\left( ten \right)=-3f\left( {2\left( {x+4} \right)} \right)+ten=g\left( x \right)=-3f\left( {\left( {\frac{1}{{\frac{1}{2}}}} \right)\left( {x-\left( {-iv} \right)} \right)} \right)+10\) would result in a coordinate rule of \({\left( {x,\,y} \right)\to \left( {.5x-4,-3y+ten} \correct)}\). (You may likewise see this as \(g\left( 10 \correct)=a\cdot f\left( {b\left( {x-h} \right)} \right)+1000\), with coordinate rule \(\displaystyle \left( {x,\,y} \right)\to \left( {\frac{1}{b}x+h,\,ay+yard} \right)\); the cease result will be the aforementioned.)
Yous may be given a random bespeak and requite the transformed coordinates for the signal of the graph. For case, if the betoken \(\left( {eight,-2} \correct)\) is on the graph \(y=g\left( 10 \right)\), give the transformed coordinates for the betoken on the graph \(y=-6g\left( {-2x} \right)-ii\). To do this, to get the transformed \(y\), multiply the \(y\) function of the bespeak by –half-dozen and then subtract two . To get the transformed \(x\), multiply the \(x\) part of the point by \(\displaystyle -\frac{1}{2}\) (reverse math). The new indicate is \(\left( {-4,x} \right)\). Let's do another example: If the point \(\left( {-4,1} \right)\) is on the graph \(y=g\left( 10 \right)\), the transformed coordinates for the bespeak on the graph of \(\displaystyle y=2g\left( {-3x-2} \right)+3=2g\left( {-3\left( {x+\frac{2}{3}} \right)} \right)+three\) is \(\displaystyle \left( {-four,ane} \right)\to \left( {-iv\left( {-\frac{1}{3}} \correct)-\frac{ii}{3},2\left( 1 \right)+3} \correct)=\left( {\frac{2}{3},5} \right)\) (using coordinate rules \(\displaystyle \left( {x,\,y} \correct)\to \left( {\frac{ane}{b}ten+h,\,\,ay+k} \right)=\left( {-\frac{1}{3}x-\frac{2}{three},\,\,2y+3} \correct)\)).
You may as well be asked to transform a parent or non-parent equation to go a new equation. We can do this without using a t-chart, but by using substitution and algebra. For example, if we want to transform \(f\left( 10 \correct)={{x}^{2}}+iv\) using the transformation \(\displaystyle -2f\left( {x-1} \right)+three\), we can simply substitute "\(x-1\)" for "\(ten\)" in the original equation, multiply by –2 , and then add 3 . For example: \(\displaystyle -2f\left( {x-1} \right)+iii=-2\left[ {{{{\left( {x-1} \correct)}}^{2}}+4} \right]+3=-2\left( {{{ten}^{2}}-2x+1+4} \correct)+3=-two{{x}^{2}}+4x-7\). We used this method to help transform a piecewise function here.
Transformations in Function Annotation (based on Graph and/or Points).
You may likewise be asked to perform a transformation of a function using a graph and individual points; in this example, you'll probably exist given the transformation in office notation. Note that nosotros may need to use several points from the graph and "transform" them, to brand sure that the transformed part has the correct "shape".
Here are some examples; the 2nd example is the transformation with an absolute value on the \(x\); see the Accented Value Transformations department for more detail.
| Original Graph and Points of Part | Transformation Example | Transformation Instance | ||||||||||||||||||||
| Original Function: Domain: \(\left[ {-four,5} \right]\) Range: \(\left[ {-seven,v} \correct]\) Cardinal Points:
Retrieve to describe the points in the same social club as the original to brand it easier! If y'all're having problem drawing the graph from the transformed ordered pairs, just take more than points from the original graph to map to the new one! | Transformation:\(\displaystyle f\left( {-\frac{1}{ii}\left( {x-1} \right)} \right)-3\) \(y\) changes:\(\displaystyle f\left( {-\frac{ane}{2}\left( {10-1} \right)} \right)\color{blue}{{-\text{ }3}}\) \(x\) changes:\(\displaystyle f\left( {\color{blue}{{-\frac{1}{2}}}\left( {x\text{ }\color{blue}{{-\text{ }i}}} \right)} \right)-iii\) Note that this transformation flips effectually the \(\boldsymbol{y}\)– axis, has a horizontal stretch of 2 , moves correct by 1 , anddown by three . Key Points Transformed: (nosotros practice the "opposite" math with the "\(x\)")
Transformed Function: Domain: \(\left[ {-9,ix} \correct]\) Range: \(\left[ {-10,2} \right]\) | Transformation: \(\displaystyle f\left( {\left| 10 \right|+ane} \right)-2\) \(y\) changes: \(\displaystyle f\left( {\left| x \right|+one} \right)\color{blueish}{{\underline{{-\text{ }2}}}}\) \(x\) changes:\(\displaystyle f\left( {\colour{blue}{{\underline{{\left| 10 \right|+1}}}}} \right)-2\): Note that this transformation moves down past 2 , and left 1 . Then, for the inside absolute value, we will "get rid of" any values to the left of the \(y\)-centrality and supercede with values to the correct of the \(y\)-axis, to brand the graph symmetrical with the \(y\)-axis. Nosotros do the absolute value part last, since it'southward only around the \(x\) on the within. Allow's just do this one via graphs. Kickoff, move down two , and left ane : Then reflect the correct-paw side across the \(y\)-axis to make symmetrical. Transformed Function: Domain: \(\left[ {-4,4} \right]\) Range:\(\left[ {-ix,0} \right]\) |
Writing Transformed Equations from Graphs
You might be asked to write a transformed equation, requite a graph. A lot of times, you can merely tell by looking at it, simply sometimes y'all have to apply a indicate or two. And you do have to be conscientious and check your work, since the lodge of the transformations tin matter.
Notation that when figuring out the transformations from a graph, it'south difficult to know whether y'all have an "\(a\)" (vertical stretch) or a "\(b\)" (horizontal stretch) in the equation \(\displaystyle yard\left( x \correct)=a\cdot f\left( {\left( {\frac{1}{b}} \right)\left( {x-h} \correct)} \right)+chiliad\). Sometimes the problem volition indicate what parameters (\(a\), \(b\), so on) to look for. For others, like polynomials (such as quadratics and cubics), a vertical stretch mimics a horizontal compression, so it'due south possible to factor out a coefficient to turn a horizontal stretch/compression to a vertical compression/stretch. (For more complicated graphs, you may desire to have several points and perform a regression in your calculator to get the office, if you're allowed to practice that).
Here are some problems. Note that atransformed equation from an absolute value graph is in the Absolute Value Transformationssection.
| Transformed Graph | Getting Equation |
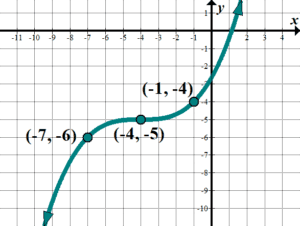
| Write the general equation for the cubic equation in the form: \(\displaystyle y={{\left( {\frac{ane}{b}\left( {ten-h} \right)} \right)}^{3}}+k\). | Nosotros come across that that the center point, or critical signal is at \(\left( {-4,-v} \right)\), so the cubic is in the course: \(\displaystyle y={{\left( {\frac{i}{b}\left( {x+4} \right)} \right)}^{iii}}-v\). Observe that to become back and over to the next points, we become dorsum/over \(3\) and down/up \(i\), and then nosotros see there's a horizontal stretch of \(three\), so \(b=iii\). (Nosotros could accept also used another point on the graph to solve for \(b\)). We take \(\displaystyle y={{\left( {\frac{1}{3}\left( {10+4} \right)} \right)}^{3}}-5\). Try it – information technology works! Note that if we wanted this function in the grade \(\displaystyle y=a{{\left( {\left( {x-h} \right)} \correct)}^{iii}}+k\), we could apply the point \(\left( {-7,-6} \correct)\) to get \(\displaystyle y=a{{\left( {\left( {x+iv} \right)} \right)}^{three}}-5;\,\,\,\,-six=a{{\left( {\left( {-vii+four} \right)} \correct)}^{iii}}-5\), or \(\displaystyle a=\frac{ane}{{27}}\). This makes sense, since if nosotros brought the \(\displaystyle {{\left( {\frac{1}{3}} \right)}^{3}}\) out from above, information technology would exist \(\displaystyle \frac{1}{{27}}\)!) |
| Observe the equation of this graph in any class: | Here's a generic method you can typically use: We see that this is a cubicpolynomial graph (parent graph \(y={{x}^{3}}\)), but flipped around either the \(x\) the \(y\)-axis, since it'south an odd function; let's employ the \(x\)-axis for simplicity's sake. The equation volition be in the form \(y=a{{\left( {x+b} \right)}^{3}}+c\), where \(a\) is negative, and it is shifted up \(2\), and to the left \(ane\). Now we take \(y=a{{\left( {x+one} \correct)}^{3}}+2\). We need to find \(a\); use the indicate \(\left( {one,-10} \right)\): \(\brainstorm{align}-ten&=a{{\left( {ane+1} \right)}^{3}}+2\\-10&=8a+2\\8a&=-12;\,\,a=-\frac{{12}}{eight}=-\frac{3}{ii}\end{align}\). The equation of the graph is: \(\displaystyle y=-\frac{3}{ii}{{\left( {x+1} \right)}^{three}}+2\). Be sure to bank check your respond by graphing or plugging in more than points! √ |
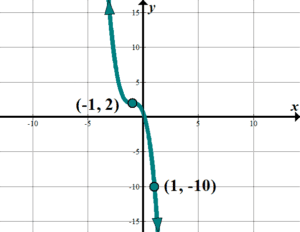
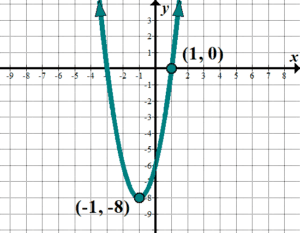
| Discover the equation of this graph in any form: | The graph looks like a quadratic with vertex \(\left( {-one,-8} \correct)\), which is a shift of \(viii\) down and \(1\) to the left. This will give us an equation of the form \(y=a{{\left( {ten+1} \right)}^{ii}}-8\), which is (not so coincidentally!) the vertex form for quadratics. Nosotros need to find \(a\); utilize the bespeak \(\left( {1,0} \right)\):\(\brainstorm{align}y&=a{{\left( {x+1} \right)}^{2}}-8\\\,0&=a{{\left( {one+1} \correct)}^{two}}-8\\viii&=4a;\,\,a=2\finish{align}\). The equation of the graph so is: \(y=2{{\left( {ten+1} \right)}^{2}}-8\). Notation: we could have also noticed that the graph goes over \(i\) and up \(two\) from the vertex, instead of over \(1\) and up \(i\) ordinarily with \(y={{x}^{ii}}\). This would mean that our vertical stretch is \(2\). |
| Find the equation of this graph in any form: | The graph looks like a rational with the "center" of asymptotes at \(\left( {-ii,three} \right)\), which is a shift of 2 to the left and 3 upward. This volition give us an equation of the class \(\displaystyle y=a\left( {\frac{1}{{x+ii}}} \right)+iii\), with asymptotes at \(10=-2\) and \(y=iii\). We need to detect \(a\); utilise the given signal \((0,iv)\): \(\begin{marshal}y&=a\left( {\frac{i}{{10+two}}} \right)+3\\4&=a\left( {\frac{1}{{0+2}}} \correct)+three\\one&=\frac{a}{2};\,a=2\terminate{align}\). The equation of the graph is: \(\displaystyle y=two\left( {\frac{one}{{x+2}}} \right)+3,\,\text{or }y=\frac{two}{{x+2}}+iii\). Notation: we could have also noticed that the graph goes over one and up 2 from the center of asymptotes, instead of over 1 and upward one unremarkably with \(\displaystyle y=\frac{ane}{10}\). This would mean that our vertical stretch is 2 . |
| Find the equation of this graph with a base of \(.five\) and horizontal shift of \(-i\): | We encounter that thisexponential graph has a horizontal asymptote at \(y=-3\), and with the horizontal shift, we take \(y=a{{\left( {.5} \right)}^{{x+1}}}-iii\) then far. When yous have a problem like this, first use any signal that has a " 0 " in it if you tin can; it volition be easiest to solve the organisation. Solve for \(a\) first using point \(\left( {0,-1} \right)\): \(\begin{array}{c}y=a{{\left( {.5} \right)}^{{10+1}}}-3;\,\,-1=a{{\left( {.5} \right)}^{{0+1}}}-3;\,\,\,\,two=.5a;\,\,a=4\\y=4{{\left( {.5} \right)}^{{ten+1}}}-three\finish{array}\) Note that there are more examples of exponential transformations here in the Exponential Functions section, and logarithmic transformations here in the Logarithmic Functions department. |
Rotational Transformations
Y'all may be asked to perform a rotation transformation on a function (you lot usually see these in Geometry form). A rotation of 90° counterclockwise involves replacing \(\left( {x,y} \correct)\) with \(\left( {-y,x} \right)\), a rotation of 180° counterclockwise involves replacing \(\left( {x,y} \correct)\) with \(\left( {-x,-y} \right)\), and a rotation of 270° counterclockwise involves replacing \(\left( {x,y} \correct)\) with \(\left( {y,-x} \right)\). Hither is an example:
| Transformation | Example | Graph | ||||||||||||
| Rotate graph 270° counterclockwise | Parent: \(y={{x}^{2}}\) Replace \((x,y)\) with \((y,–x)\)
|  Rotated Office Domain: \(\left[ {0,\infty } \right)\) Range:\(\left( {-\infty ,\infty } \correct)\) |
Transformations of Inverse Functions
Nosotros learned virtually Inverse Functions here, and y'all might be asked to compare original functions and inverse functions, as far as their transformations are concerned. Remember that an inverse function is one where the \(x\) is switched by the \(y\), so the all the transformations originally performed on the \(x\) will be performed on the \(y\):
Problem:
If a cubic part is vertically stretched by a factor of 3 , reflected over the \(\boldsymbol {y}\)-axis, and shifted downward 2 units, what transformations are done to its inverse function?
Solution:
Nosotros need to do transformations on the opposite variable. Thus, the inverse of this function will exist horizontally stretched by a factor of 3 , reflected over the \(\boldsymbol {ten}\)-axis, and shifted to the left two units. Here is a graph of the two functions:
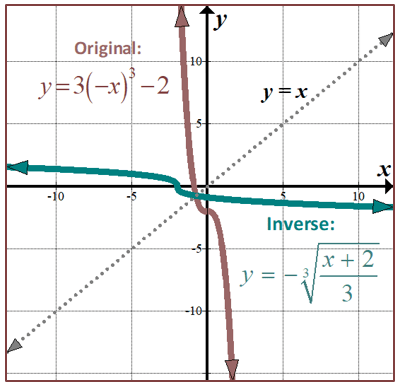
Note that examples of Finding Inverses with Restricted Domains tin be found here.
Applications of Parent Role Transformations
You may come across a "word trouble" that used Parent Function Transformations, and you can utilize what you know about how to shift a function. Here is an example:
| Transformation Awarding Trouble | Solution |
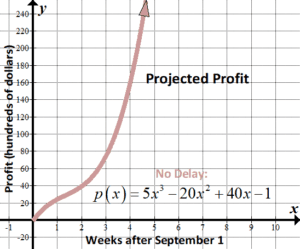
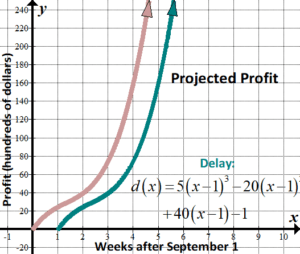
| The following polynomial graph shows the turn a profit that results from selling math books after September 1. The polynomial is \(p\left( 10 \right)=5{{x}^{iii}}-20{{x}^{2}}+40x-1\), where \(x\) is the number of weeks afterwards September 1. The publisher of the math books were one week behind notwithstanding; depict how this new graph would look and what would be the new (transformed) function? | Since we're moving the time in weeks past 1 week, we are shifting the graph horizontally, or shifting the inside, or \(x\) values. Since our showtime profits volition outset a picayune afterwards calendar week one , we can see that we need to motility the graph to the right. When we move the \(ten\) part to the correct, we take the \(x\) values and subtract from them, and then the new polynomial will be \(d\left( 10 \correct)=v{{\left( {10-1} \right)}^{iii}}-xx{{\left( {x-i} \right)}^{2}}+forty\left( {x-1} \right)-1\). (I won't multiply and simplify.) See how this was much easier, knowing what nosotros know about transforming parent functions? |
Larn these rules, and practice, practise, exercise!
For Practice: Use the Mathway widget below to try aTransformation problem. Click on Submit (the blueish arrow to the right of the problem) and click on Describe the Transformation to see the answer.
You tin can too type in your own problem, or click on the three dots in the upper right manus corner and click on "Examples" to drill downward past topic.
If you lot click on Tap to view steps, or Click Hither, you can register at Mathway for a gratuitous trial, and then upgrade to a paid subscription at whatever time (to get whatsoever blazon of math problem solved!).
On to Accented Value Transformations – you are gear up!
Source: https://mathhints.com/parent-graphs-and-transformations/
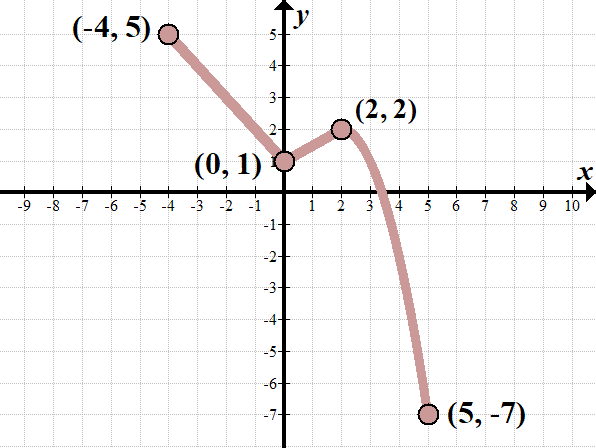
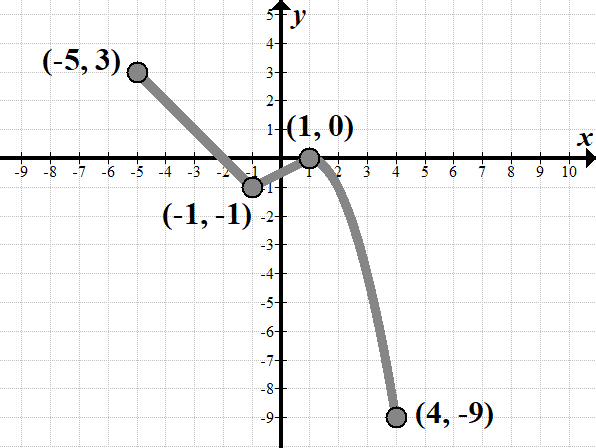
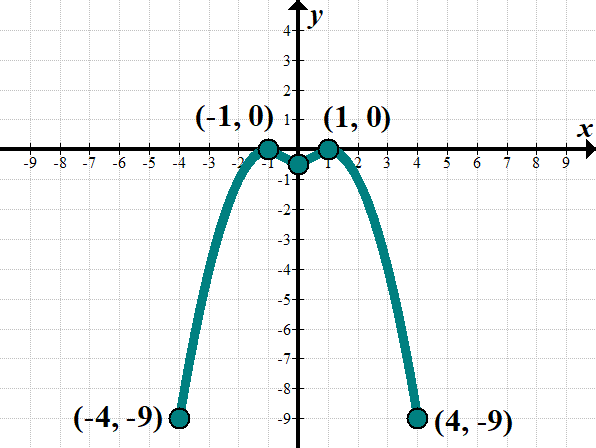
0 Response to "What Parent Function Goes Up Down and Up Again on a Graph"
Post a Comment